2007年中国科学院金属研究所张志东研究员在英国《哲学杂志》(Philosophical Magazine)上发表论文,提出两个猜想,并在猜想基础上推定出三维伊辛模型的精确解。被《哲学杂志》审稿人评价为“过去几十年间,三维伊辛模型领域的最重要进展……可作为三维伊辛情况精确描述的一个基准”。论文发表后在国际学术界引起了强烈反响和学术争鸣。最近,张志东研究员在三维伊辛模型精确解研究方面又取得新的进展。他与日本数学家日本大学的铃木理(Osamu Suzuki)教授、英国物理学家牛津大学的诺曼 马赫(Norman H. March)教授合作,发展了一个三维伊辛模型的克利福德代数方法,通过证明四个定理,从正面支持了之前提出的两个猜想,进而表明在两个猜想基础上推定的精确解是正确的。张志东研究员在最近的工作中证明了如下四个定理:
定理一 (迹不变定理):当在原始的转移矩阵中的直乘增加k项单位矩阵,三维伊辛模型的配分函数改变一个因子2k 。通过除法抵消这个2k因子,以保持迹不变。调节单位矩阵与其他矩阵的次序以分隔转移矩阵中不同排的e指数因子 (每排包含 n 个晶格点)。每排的e指数因子被单位矩阵隔离开来,以致它们可以被看成转移矩阵的分矩阵而被分别处理。
定理二 (线性化定理):对三维伊辛模型的每一排的分矩阵进行一个线性化过程。局部地,每一排的分矩阵中的非线性项可以被线性化。
定理三 (局域变换定理):对三维伊辛模型的每一排的分转移矩阵进行一个局域变换。局域变换改变局部系统的规范,平庸化系统的非平庸拓扑结构,同时在三维伊辛模型的本征矢量上产生拓扑相因子。
定理四 (对易性定理):在三维伊辛模型线性化过程和局域变换过程中算符的非对易性性质可以在约当-冯 诺依曼-维格纳机制的框架中应用约当代数处理成对易,通过对在时空中演化的三维伊辛模型的t个系统进行时间平均来实现。
题目为《三维伊辛模型的克利福德代数方法》的论文发表在国际数学刊物《应用克利福德代数研究进展》(Advances in Applied Clifford Algebras)上。这项工作从正面支持了张志东研究员于2007年提出的两个猜想,表明在两个猜想基础上推定的精确解是正确的。这项工作建立了拓扑量子统计物理学;利用约当代数、时间平均,在(3+1)维度的约当-冯 诺依曼-维格纳机制框架内,通过拓扑变换和规范变换来处理三维多体相互作用体系的非平庸拓扑学问题。并且发现了三维多体相互作用体系的拓扑相因子。对理解物质之间的相互作用、拓扑学对物理性质的贡献、空间的本质、时间的自发产生等具有启发性的指导作用。相关工作对凝聚态物理、统计物理、高能物理、生物、计算机科学等领域的研究有着促进作用。
有序和无序是自然界普遍存在的两种状态,它们既矛盾对立又相互转化。在两个状态转变之间存在一个临界点。临界点附近存在着一些丰富有趣的临界现象。临界现象广泛存在于自然界中,例如,铁磁材料从顺磁态到铁磁态的转变;某些合金从无序到有序的转变;超导体从正常态到超导态的转变;水以及许多液体材料的临界点存在液态-气态共存;液体-液体两相体系中也存在两相共存的临界点,甚至生物体中DNA的折叠、病毒的传播、人工智能体系的计算,都存在着有序和无序的相变和临界现象。
伊辛模型是描述临界现象的一个基本模型,它考虑每一个自旋有两种可能的状态(自旋向上和自旋向下),自旋和自旋之间存在相互作用。伊辛模型可被推广用于研究连续的量子相变、基本粒子的超弦理论、动力学临界行为等。原则上,伊辛模型可以描述具有两种可能状态的个体,个体之间存在相互作用组成的多体体系。它甚至可以描述森林火灾、交通堵塞、股市涨落、舆情传播等社会学、经济学现象。
1920年德国科学家楞次教授提出“伊辛模型”,1925年楞次教授的学生伊辛发表了一维伊辛模型的精确解,所以该模型也被称为“楞次-伊辛模型”。这个方面的一个重要进展发生在1944年,美国科学家昂萨格教授得出了二维伊辛模型的精确解,第一次显示从非奇异性的哈密顿量出发可以在临界点出现物理函数的奇异性,被视作统计物理的重大进展。但是昂萨格的求解方法无法直接应用到三维伊辛模型的精确求解,遇到的根本性困难是在三维伊辛模型中存在着拓扑学问题。这个问题困扰了学术界近百年。
张志东研究员在科学网博客中以《追梦之旅》、《激辩猜想》、《终结猜想》三个系列的博文对三维伊辛模型精确解的求解过程和相关结果进行了科普。欢迎广大同行和科学爱好者对此项工作开展进一步的学术讨论和交流。
三维伊辛模型精确解研究相关论文链接:
1. 提出两个猜想:Z.D. Zhang, Philosophical Magazine 87 (2007) 5309. 链接1
2. 初探数学结构:Z.D. Zhang, Chinese Physics B 22 (2013) 030513. 链接2
3. 证明四个定理:Z.D. Zhang, O. Suzuki and N.H. March, Advances in Applied Clifford Algebras 29 (2019) 12. 链接3
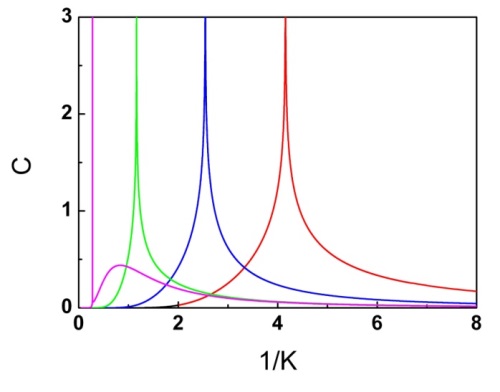
三维伊辛模型的精确解:不同相互作用参数条件下比热与温度的依赖关系